Explorez. Modélisez. Optimisez
Au travers des prestations de service ou missions de freelance, nous aidons les startups et les entreprises à explorer des solutions d’optimisation pour relever leurs défis.
États de l’art, Modélisation sur mesure, Preuves de Concept (PoC)
Tarif Freelance TJM: 550€
Expert Freelance en Recherche opérationnelle (optimisation et développement d’algorithmes) avec une solide expérience dans la résolution de problèmes complexes.
Outils: Solveurs d’optimisation Cplex, Scip, Gurobi
Langages de programmation: Python & C++
Nos Services

L’État de l’Art
Cela consiste à situer votre problème dans la littérature scientifique et les pratiques actuelles pour garantir des solutions adaptées et innovantes.
Nous effectuons une revue approfondie des travaux existants, en explorant :
Les approches mathématiques et algorithmiques utilisées dans des cas similaires.
Pourquoi est-ce important ?
Cette analyse nous permet de comprendre ce qui a déjà été fait, de mettre en lumière les limites des solutions existantes et d’identifier les opportunités d’innovation. En nous appuyant sur les avancées de la recherche, nous vous proposons la meilleure approche possible pour résoudre votre problème.

Modélisation Mathématique
La modélisation mathématique est au cœur de l’optimisation des problèmes complexes. Grâce à une approche rigoureuse, nous traduisons les problématiques de votre entreprise en modèles mathématiques précis, permettant d’identifier les contraintes et variables clés de vos systèmes. Que ce soit pour optimiser la gestion de la chaîne logistique, la répartition des ressources ou encore la planification stratégique, nos modèles permettent de simuler divers scénarios et de prendre des décisions informées basées sur des analyses quantitatives. Nous travaillons sur des modèles linéaires, non-linéaires, stochastiques, ainsi que sur des systèmes dynamiques pour couvrir un large éventail de problématiques.
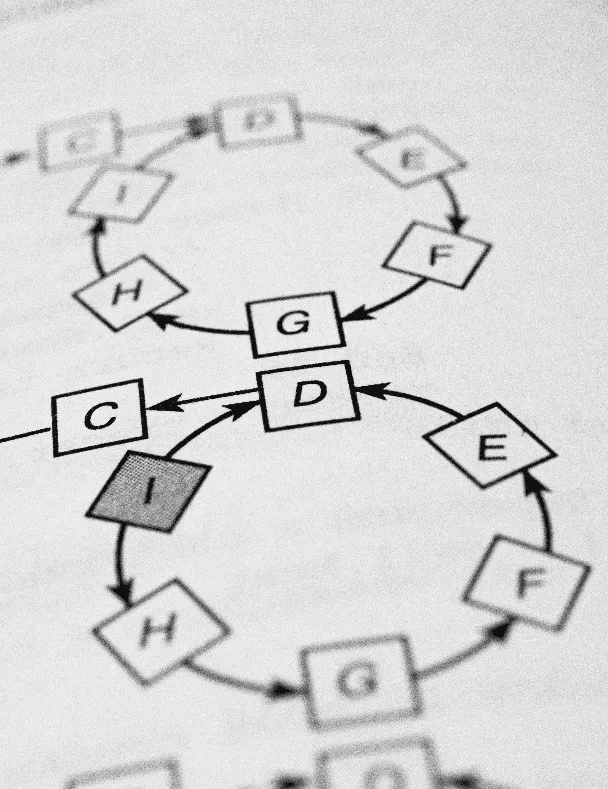
Développement d’Algorithme
Nous concevons des algorithmes avancés pour résoudre vos problèmes d’optimisation avec précision et efficacité. Nous maîtrisons des techniques exactes comme la génération de colonnes, idéale pour décomposer les problèmes complexes, la décomposition de Benders, qui simplifie les modèles multi-niveaux, et les cutting planes, pour accélérer la convergence vers des solutions optimales.
Pour des solutions rapides et adaptées, nous utilisons également des métaheuristiques telles que les algorithmes génétiques ou le recuit simulé, capables de fournir des résultats performants en un temps limité.

La programmation linéaire
L’optimisation linéaire résout des problèmes où la fonction objectif et les contraintes sont linéaires. Très utilisée en optimisation, elle optimise les coûts et les ressources dans la logistique, la finance et l’industrie.

La programmation non-linéaire
L’optimisation non linéaire traite des problèmes où les relations entre les variables ne sont pas linéaires. Elle est employée dans l’énergie, l’ingénierie et la finance, utilisant des algorithmes avancés pour des systèmes complexes.

Les algorithmes de décomposition
Les algorithmes de décomposition divisent des problèmes complexes en sous-problèmes plus simples. Les méthodes, comme Benders ou Dantzig-Wolfe, sont appliquées dans les réseaux, la logistique et l’énergie pour des solutions rapides.

Les Metaheuristiques et les Matheuritiques
Les métaheuristiques explorent efficacement des solutions pour des problèmes complexes. Les matheuristiques, intégrant des approches exactes, sont populaires pour des solutions hybrides performantes.
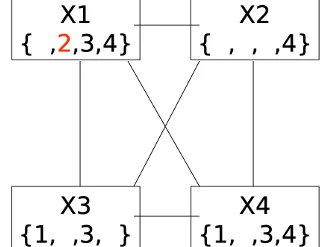
La programmation par contraintes
La programmation par contraintes modélise des problèmes combinatoires complexes. Elle est, souvent, utilisée pour la planification et l’automatisation, permettant la prise des décisions précises et efficaces.